This article presents a C++ doubly linked list system that is based on an earlier article.
It is natural to ask what is the point of using doubly linked lists when singly linked lists or arrays could be used.
Singly linked lists and doubly linked lists can be efficiently traversed in both the forward and backward* directions. Given a pointer x to a list node, doubly linked lists can in O(1) steps insert and/or delete at x whereas singly linked lists need to search the entire list for the "previous" node therefore taking O(n) steps for the same result. In particular inserting or deleting at the end of the list takes O(1) time for doubly linked lists and O(n) time for singly linked lists. If insertions and/or deletions are done as part of a traversal, then the programmer can keep track of the previous pointer and traverse the singly linked list in the forward direction with optional insertions and/or deletions in O(n) time. Doubly linked lists also take O(n) time for the same operation but do not need the extra complexity of maintaining a previous pointer. Both types of linked lists need a temporary variable when traversing with optional deletions. See below for how to achieve this with doubly linked lists.
For some operations singly linked lists are marginally faster than doubly linked lists, since doubly linked lists have an extra pointer per node (called previous), which means for more pointer manipulations inside the doubly linked list classes. In spite of this extra complexity the difference in terms of big-O notation is zero. Assuming that the extra complexity for the manipulation of doubly linked lists can be subsumed into an abstract data type, then doubly linked lists are simpler than or as simple as singly linked lists.
The above remarks indicate that doubly linked lists are superior to singly linked lists. What follows is a comparison between doubly linked lists and arrays. Doubly linked lists can be traversed in O(n) time in either direction just like arrays. In addition to this, given a pointer to a node x of a list, insertions and deletions at x can be done in O(1) time. Given an index i of an array insertions and deletions at i take O(n) time.
Doubly linked lists have two disadvantages compared to arrays. Firstly, random access of a list takes O(n) time compared with O(1) time for arrays. This is not a disadvantage if the list can be processed via a traversal which accesses all elements in O(n) time, the same speed as arrays. Secondly, searching for an element in a (singly or doubly) linked list takes O(n) time, whereas searching for an element in a pre-sorted array takes O(log(n)) time.
If fast random access and fast searching is required in addition to fast traversal, insertion and deletion, then the programmer should use AVL trees or one of the other various types of trees. Like doubly linked lists, trees support efficient traversal, insertion and deletion. Like arrays, trees support efficient traversal, random access and searching.
To support the above remarks, consider the following table that compares the computation times for pre-sorted arrays, singly linked lists, doubly linked lists, and AVL trees:
| Pre-sorted Arrays | Singly Linked Lists | Doubly Linked Lists | AVL Trees | |
|---|---|---|---|---|
| Forward Traversal | O(n) | O(n) | O(n) | O(n) |
| Backward Traversal | O(n) | O(n)* | O(n) | O(n) |
| Forward Traversal with insertions and/or deletions | O(n) * O(n) = O(n2) | O(n) | O(n) | O(n) * O(log(n)) = O(nlog(n)) |
| Insertion or deletion at end | O(1) | O(n) | O(1) | O(log(n)) |
| Insertion at a given index/node | O(n) | O(n) | O(1) | O(log(n)) |
| Deletion at a given index/node | O(n) | O(n) | O(1) | O(log(n)) |
| Random Access | O(1) | O(n) | O(n) | O(log(n)) |
| Searching for a given element | O(log(n)) | O(n) | O(n) | O(log(n)) |
NOTE: * indicates that singly linked lists can be traversed in O(n) operations in the backward direction via a stack recursion. With doubly linked lists, backward traversal can be achieved using iteration which is simpler and uses less stack memory than recursion.
This diagram is borrowed from an earlier article.
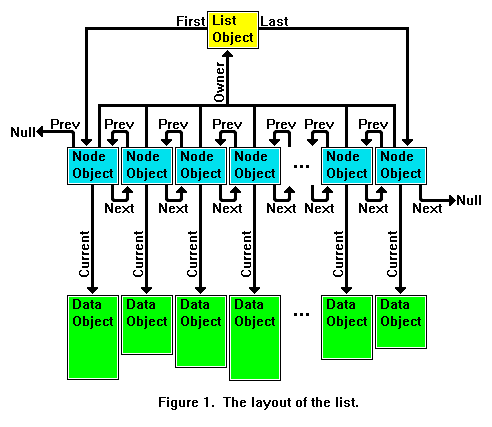
A major change has been made to the Node<X> template class from an earlier article. In the old system the property current was defined to be public of type X like so:
public: X current |
In the new system, the property current has been renamed to private_data and has been defined to be private of type X* with one setter and two getter methods for getting/setting the value of private_data. Also the property private_dirty is set if a non-const pointer to the list internals is returned or if the list is altered via the set_data() method like so:
private:
X* private_data;
public:
const X* get_data_const() const
{
return private_data;
}
X* get_data()
{
private_dirty = true;
return private_data;
}
void set_data(X* x)
{
private_dirty = true;
private_data = x;
}
|
Under the earlier system, the user could choose X to be either a pointer or a non-pointer variable. If the user chose X to be a pointer property variable, then the responsibility for calling operator delete on the current property lies with the user of the doubly linked list system. On the other hand, if the user chose X to be a non-pointer property variable, then the deleting of current is done automatically whenever Node objects are deleted.
Under the new system presented in this article, the property private_data is defined to be of type X*, i.e. a pointer variable. This is a more restrictive system than the previous one as the choice between a pointer or a non-pointer variable no longer exists. The new system has the advantage that three macros of the earlier system: INSTANTIATE_OUTPUT_PROTOTYPE, INSTANTIATE_OUTPUT_DEFINITION and INSTANTIATE_OUTPUT_DEFINITION_STAR are no longer required. There is another advantage of having private_data to be of type X* and that is that the method get_data_const() can be defined as returning a const X*. If private_data was of type X then the method get_data_const() could not be defined like so.
Using a naming convention like naming certain variables with a prefix enables syntax highlighting to be defined on them using the Emacs text editor.
Another improvement of the previous system, this system keeps track of the length of the lists in the private property private_length. This property can be returned to the client code by a call to the method get_length(). This allows the list's length to be determined in O(1) time, compared with O(n) time for the previous system.
Another improvement to the previous system is that the private property variable private_dirty keeps track of whether or not the list has been altered since construction, or since the most recent call to the clear_dirty() method, which sets private_dirty to false. Read access to this property is provided by the get_dirty() method. If get_dirty() returns false, it can be assumed that the list is unchanged and therefore values computed from the list do not need to be recalculated.
However this system is not completely fool-proof. If a non-const pointer to the list internals is returned, followed by a call to the clear_dirty() method, then it is possible for the list internals to be altered while the value of get_dirty() returns false. It is the duty of the client code to make sure this does not happen. Therefore non-const pointers to the list internals should be used with care.
The following macros are defined:
|
Defines a forward non-const iteration through argument list. |
|
Defines a forward const iteration through argument list. |
|
Defines a backward non-const iteration through argument list. |
|
Defines a backward const iteration through argument list. |
Using the above macros, iteration through a linked list is very easy. Example:
int main() { List<int>* list1 = new List<int>(); // prints out 0 (meaning list1 is not dirty) cout << list1->get_dirty() << endl; list1->add_element(new int(1)); list1->add_element(new int(2)); list1->add_element(new int(3)); // prints out 1 (meaning list1 is dirty) cout << list1->get_dirty() << endl; // clears the "private_dirty" flag of list1 list1->clear_dirty(); // the following code prints out 1 2 3 for_list_const (int,n,list1) { cout << *n << " "; } cout << endl; // prints out 0 (meaning list1 is not dirty) cout << list1->get_dirty() << endl; // the following code prints out 3 2 1 for_list_backwards_const (int,n,list1) { cout << *n << " "; } cout << endl; // prints out 0 (meaning list1 is not dirty) cout << list1->get_dirty() << endl; List<int>* list2 = new List<int>(); list2->add_element(new int(4)); list2->add_element(new int(5)); list2->add_element(new int(6)); for_list_backwards (int,n,list1) { list2->add_to_start(n); } // prints out 1 (meaning list1 is dirty) cout << list1->get_dirty() << endl; // prints out 1 (meaning list2 is dirty) cout << list2->get_dirty() << endl; // clears the "private_dirty" flag of list2 list2->clear_dirty(); // prints out 1 2 3 4 5 6 for_list_const (int,n,list2) { cout << *n << " "; } cout << endl; // prints out 0 (meaning list2 is not dirty) cout << list2->get_dirty() << endl; // deletes all "private_data" fields in list2 list2->delete_deep(); // delete all nodes in list2 delete list2; // list1->delete_deep() is not called since // all data objects on list1 are also on list2 // deletes all nodes in list1 delete list1; } |
Traversing a doubly linked list with optional deletions cannot use the above-mentioned iterator macros. Instead a Node<X>* variable (which I will call n_next) is required to store the private_next property in case the current node is deleted.
Node<X>* n_next; for (Node<X>* n = list->get_first(); n != null; n=n_next) { n_next = n->get_next(); if (/* arbitrary bool valued expression */) { delete n; // n->get_next() is no longer valid but n_next is valid } } |
Add the following lines of Emacs Lisp code to your .emacs file to achieve correct syntax highlighting of the iterator macros:
|
The doubly linked list system is comprised of two main template classes List<X> and Node<X> and four extra template classes: List_Extra<X>, List_Io<X>, List_Operator_Ee<X> and List_Clone<X>. These classes can be instantiated with six lines of code:
template class List<X>; template class Node<X>; template class List_Extra<X>; template class List_Io<X>; template class List_Operator_Ee<X>; template class List_Clone<X>; |
where X is the argument to the template. The last four classes are collections of friend functions. The reason they have been put in classes is to reduce the number of lines of template instantiation that are required to use the linked list system. If the functions of these four classes had been stand-alone global functions, then one line of template instantiation per function would be required, making the system rather cumbersome to use.
If some of these last four template classes are not required by the client code, then their lines of template instantiation can be omitted, giving the client finely grained control over which functions and/or classes are to be used. Here are the UML diagrams of the above-mentioned classes:
|
Represents the doubly linked list. Deletions of a List<X> object causes deletions of all Node<X> objects in the linked list, starting at private_first and ending at private_last. Deletions of the private_data property (of type X*) are not carried out, since the X object referred to could be on more than one linked list. Notwithstanding this, it is the responsibility of the client to delete the X objects when they are no longer required. The List<X> method delete_deep() deletes all X objects on the given list. The client must keep track of all X objects that have been constructed, possibly by having one "special" linked list to hold all the X objects and calling delete_deep() on that list when they are no longer required. |
|||
|
Represents nodes of the doubly linked list. Importantly the Node<X> constructor is private, so the Node<X> objects may only be created indirectly via calls the the methods: add_element(), add_to_start(), add_to_end(), add_after_current() and add_before_current(). Deletions of Node<X> objects cause the removal of that node (and X object) from the linked list. However deletions of Node<X> objects does not result in deletions of private_data, since (as above) the X object referred to could be on more than one linked list. To delete the X object of a Node<X> called n use the following statement:
One should note after the above statement the list is in a fragile state because n->private_data now points to unallocated memory. Therefore there are only two sensible statements that can follow this one. Here is the first option:
which deletes the node without touching n->private_data. The second option is to change n->private_data to null (or some other sensible value) like so:
|
|||
|
The template class List_Extra<X> should be instantiated whenever one of its functions need to be used. The functions within the class are inessential to the doubly linked list system, but useful nonetheless. |
|||
|
The template class List_Io<X> should be instantiated only if my non-standard file I/O library is to be used. This library is explained in another article. This template class also assumes that a function
has been defined. |
|||
|
The template class List_Operator_Ee<X> should be instantiated only if operator == (const X&, const X&) has been defined for the X class. The functions within this class use this operator for comparing X objects. |
|||
|
The template class List_Clone<X> should be instantiated only if the function X* clone(X&) has been defined. If defined, it should return the same result as X(const X&). |
|
list.hh |
|
t-list.cc |
|
t-list.el |
|
list2.tar.gz |
| Back to Research Projects |
|
This page has the following hit count:
|